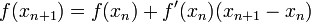ANÁLISIS NUMÉRICO
miércoles, 30 de mayo de 2012
Quieres vivir por siempre, pues la inmortalidad esta a la vuelta de la esquina
Proyecto ruso promete reemplazar el cuerpo humano por uno robótico en 2045

La inmortalidad ha sido uno de los temas centrales dentro de la ciencia ficción y ahora, una nueva iniciativa rusa busca crear robots que reemplacen nuestro cuerpo.
Rusia 2045 a presentado su programa Avatar, cuyo objetivo es conservar la mente y personalidad de las personas dentro de cerebros artificiales, los que a su vez serían colocados dentro de cuerpos robóticos. En ocho años el grupo espera crear un robot humanice que pueda se controlado directamente con el cerebro y en 2025 confían en ser capaces de realizar el transplante de cerebro directamente sobre la máquina.
El líder del programa, Dmitry Itskov señala que esos cuerpos superarán a los que tenemos en cuanto a su funcionalidad, pero que no perderán la belleza o el atractivo del cuerpo humano.
Por el momento, el equipo ha logrado construir un androide realista, sin embargo, los únicos movimientos que puede realizar son parpadear y mover sus dedos y llegar a su meta parece muy lejana.
lunes, 9 de abril de 2012
Métodos Numéricos para Ingenieros libro de Chapra pdf
Tienes problemas con la materia de análisis numérico descarga el libro de métodos numéricos para ingenieros entra a esta pagina inscribe te gratis y descarga el libro
http://www.4shared.com/get/Vlk4Lqcb/metodos_numericos_para_ingenie.html
http://www.4shared.com/get/Vlk4Lqcb/metodos_numericos_para_ingenie.html
Qué es la regla de los signos de Descartes
Supongamos que tenemos el polinomio 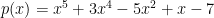 . Si igualamos
. Si igualamos 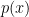 a 0 obtenemos la siguiente ecuación polinómica:
a 0 obtenemos la siguiente ecuación polinómica:
Ordenemos los coeficientes según el grado del monomio al que multiplican, colocando en primer lugar al que corresponde al de grado mayor. Obtendríamos la siguiente lista:
Obviando el cero, tenemos que en esta lista se producen tres cambios de signo: del 3al -5, del -5 al 1 y del 1 al -7. Llamando 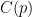 al número de cambios de signo en la lista de coeficientes del polinomio
al número de cambios de signo en la lista de coeficientes del polinomio 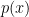 , tendríamos entonces que en este caso
, tendríamos entonces que en este caso 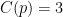 .
.
Por otra parte, si utilizamos un programa informático para calcular las raíces de dicha ecuación (bueno, aproximaciones de las mismas), obtenemos que tiene una solución real positiva y cuatro soluciones complejas (dos parejas compleja-conjugada).
Lo que hace la regla de los signos de Descartes es relacionar el número de cambios de signo en la lista de coeficientes de una ecuación polinómica con el número de raíces positivas de dicha ecuación. Por desgracia no da una cantidad exacta de soluciones, sino que nos da una cota, aunque en muchas ocasiones dicha cota puede propocionar información muy interesante sobre la cantidad de raíces positivas de la ecuación. Vamos a enunciar esta regla:
Regla de los signos de DescartesEl número de raíces reales positivas de una ecuación polinómica con coeficientes reales igualada a cero es, como mucho, igual al número de cambios de signo que se produzcan entre sus coeficientes (obviamos los ceros).
Es decir, que el número de cambios de signos que se produzcan entre los coeficientes es una cota superior del número de raíces positivas de la ecuación.
TEOREMA DE BOLZANO Y MÉTODO DE LA BISECCIÓN PARA LOCALIZAR LAS RAÍCES DE UNA FUNCIÓN
ENUNCIADO DEL TEOREMA
Si f(x) es una función continua en el intervalo [a, b], y si, además, en los extremos del intervalo la función f(x) toma valores de signo opuesto (f(a) * f(b) < 0), entonces existe al menos un valor c Î (a, b) para el que se cumple: f(c) = 0.
Es decir: si una función es continua en un intervalo cerrado y acotado [a, b], y los valores en los extremos del intervalo tienen signos distintos, entonces podemos asegurar la existencia de al menos una raiz de la función en el intervalo abierto (a, b).
Ejemplo1: La función que aparece representada a continuación es continua en el intervalo [3, 6.2] y f(3) < 0 mientras que f(6.2) >0. Como se cumplen las hipótesis del teorema de Bolzano queda garantizada la existencia de al menos un valor c en el que f(c) = 0, es decir en el que la gráfica corta al eje de abcisas. En este ejemplo concreto existen exactamente tres valores (c1, c2 y c3) que cumplen la tesis del teorema. (A los valores c1, c2 y c3 se les llama raices o ceros de la función f(x) en el intervalo en cuestión). (La función representada es: f(x) = sen(2x) - 2cos(x/3))

MÉTODO DE LA BISECCIÓN
El teorema de Bolzano tiene una interesante aplicación en la localización de las raices o ceros de una funcion continua. Consiste en lo siguiente: buscamos por tanteo dos valores "a" y "b" para los que la función tome signos opuestos. Si conseguimos encontrar dos valores que cumplan la condición anterior, por ejemplo f(a) < 0 y f(b) > 0, y, además, la función es continua en I = [a, b], queda garantizada por el teorema de Bolzano la existencia en el intervalo (a, b) de al menos una raiz. Si ahora tomamos el punto medio del intervalo (x = (a + b)/2) la función en ese punto puede tomar el valor 0, en cuyo caso ya tendríamos localizada una raiz, o bien en (a + b)/2 toma un valor positivo o negativo. Si f((a + b)/2) < 0, nos fijaríamos ahora en el intervalo
I1 =[(a + b)/2, b] en el que la función es continua y en cuyos extremos toma valores de signos opuestos. El teorema de Bolzano garantiza así la existencia de al menos una raiz en ese intervalo I1 de longitud la mitad de la longitud del intervalo inicial. (Si f((a + b)/2)>0 I1=[a, (a +b)/2]. Se repite el mismo proceso con el intervalo I1, con lo que vamos obteniendo intervalos cada vez más pequeños, dentro de los cuales sabemos que existe una raiz. Podemos así hallar el valor de esa raiz con la aproximación deseada.
Método de las aproximaciones sucesivas
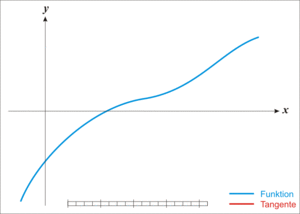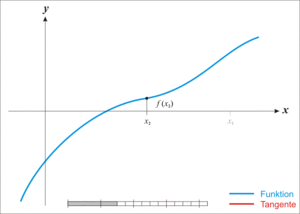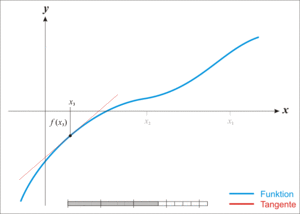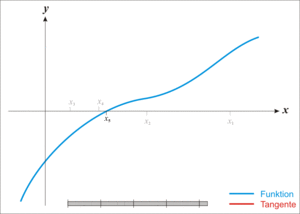
Dada la ecuación f(x) = 0, el método de las aproximaciones sucesivas reemplaza esta ecuación por una equivalente, x=g(x), definida en la forma g(x)=f(x)+x. Para encontrar la solución, partimos de un valor inicial x0 y calculamos una nueva aproximación x1=g(x0). Reemplazamos el nuevo valor obtenido y repetimos el proceso. Esto da lugar a una sucesión de valores 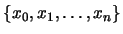 , que si converge, tendrá como límite la solución del problema.
, que si converge, tendrá como límite la solución del problema.
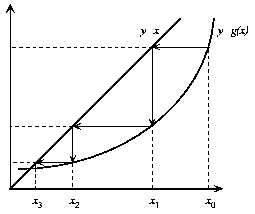
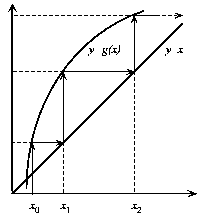
En la figura (4) se representa la interpretación geométrica del método. Partimos de un punto inicial x0 y calculamos y = g(x0). La intersección de esta solución con la recta y=x nos dará un nuevo valor x1 más próximo a la solución final.
Sin embargo, el método puede divergir fácilmente. Es fácil comprobar que el método sólo podrá converger si la derivada g'(x) es menor en valor absoluto que la unidad (que es la pendiente de la recta definida por y=x). Un ejemplo de este caso se muestra en la figura (5). Esta condición, que a priori puede considerarse una severa restricción del método, puede obviarse fácilmente. Para ello basta elegir la función g(x) del siguiente modo:
de forma que tomando un valor de 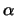 adecuado, siempre podemos hacer que g(x) cumpla la condición de la derivada.
adecuado, siempre podemos hacer que g(x) cumpla la condición de la derivada.
Método de Newton
En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.
Descripción del método
El método de Newton-Raphson es un método abierto, en el sentido de que su convergencia global no está garantizada. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la rectatangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente. f'(x)= 0 Sea f : [a, b]-> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x0 y definimos para cada número natural n
Donde f ' denota la derivada de f.
Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita cognoscible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.
Obtención del Algoritmo
Tres son las formas principales por las que tradicionalmente se ha obtenido el algoritmo de Newton-Raphson.
La primera de ellas es una simple interpretación geométrica. En efecto, atendiendo al desarrollo geométrico del método de la secante, podría pensarse en que si los puntos de iteración están lo suficientemente cerca (a una distancia infinitesimal), entonces la secante se sustituye por la tangente a la curva en el punto. Así pues, si por un punto de iteración trazamos la tangente a la curva, por extensión con el método de la secante, el nuevo punto de iteración se tomará como la abscisa en el origen de la tangente (punto de corte de la tangente con el eje X). Esto es equivalente a linealizar la función, es decir, f se reemplaza por una recta tal que contiene al punto (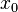 ,
, 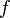 (
(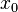 )) y cuya pendiente coincide con la derivada de la función en el punto,
)) y cuya pendiente coincide con la derivada de la función en el punto, 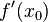 . La nueva aproximación a la raíz,
. La nueva aproximación a la raíz,  , se logra la intersección de la función lineal con el eje X de abscisas. Matemáticamente:
, se logra la intersección de la función lineal con el eje X de abscisas. Matemáticamente:
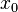 ,
, 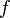 (
(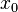 )) y cuya pendiente coincide con la derivada de la función en el punto,
)) y cuya pendiente coincide con la derivada de la función en el punto, 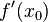 . La nueva aproximación a la raíz,
. La nueva aproximación a la raíz,  , se logra la intersección de la función lineal con el eje X de abscisas. Matemáticamente:
, se logra la intersección de la función lineal con el eje X de abscisas. Matemáticamente:
En la ilustración adjunta del método de Newton se puede ver que  es una mejor aproximación que
es una mejor aproximación que 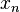 para el cero (x) de la función f.
para el cero (x) de la función f.
 es una mejor aproximación que
es una mejor aproximación que 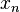 para el cero (x) de la función f.
para el cero (x) de la función f.
Una forma alternativa de obtener el algoritmo es desarrollando la función f (x) en serie de Taylor, para un entorno del punto 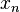 :
:
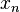 :
:
Si se trunca el desarrollo a partir del término de grado 2, y evaluamos en  :
:
 :
:
Si además se acepta que  tiende a la raíz, se ha de cumplir que
tiende a la raíz, se ha de cumplir que  , luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.
, luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.
 tiende a la raíz, se ha de cumplir que
tiende a la raíz, se ha de cumplir que  , luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.
, luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.
Finalmente, hay que indicar que el método de Newton-Raphson puede interpretarse como un método de iteración de punto fijo. Así, dada la ecuación  , se puede considerar el siguiente método de iteración de punto fijo:
, se puede considerar el siguiente método de iteración de punto fijo:
 , se puede considerar el siguiente método de iteración de punto fijo:
, se puede considerar el siguiente método de iteración de punto fijo:
Se escoge h (x) de manera que g'(r)=0 (r es la raíz buscada). Dado que g'(r) es:
Entonces:
Como h (x) no tiene que ser única, se escoge de la forma más sencilla:
Por tanto, imponiendo subíndices:
Expresión que coincide con la del algoritmo de Newton-Raphson
Convergencia del Método
El orden de convergencia de este método es, por lo menos, cuadrático. Sin embargo, si la raíz buscada es de multiplicidad algebraica mayor a uno (i.e, una raíz doble, triple, ...), el método de Newton-Raphson pierde su convergencia cuadrática y pasa a ser lineal de constante asintótica de convergencia 1-1/m, con m la multiplicidad de la raíz.
Existen numerosas formas de evitar este problema, como pudieran ser los métodos de aceleración de la convergencia tipo Δ² de Aitken o el método de Steffensen. Derivados de Newton-Raphson destacan el método de Ralston-Rabinowitz, que restaura la convergencia cuadrática sin más que modificar el algoritmo a:
Evidentemente, este método exige conocer de antemano la multiplicidad de la raíz, lo cual no siempre es posible. Por ello también se puede modificar el algoritmo tomando una función auxiliar g(x) = f(x)/f'(x), resultando:
Su principal desventaja en este caso sería lo costoso que pudiera ser hallar g(x) y g'(x) si f(x) no es fácilmente derivable.
Por otro lado, la convergencia del método se demuestra cuadrática para el caso más habitual en base a tratar el método como uno de punto fijo: si g'(r)=0, y g' '(r) es distinto de 0, entonces la convergencia es cuadrática. Sin embargo, está sujeto a las particularidades de estos métodos.
Nótese de todas formas que el método de Newton-Raphson es un método abierto: la convergencia no está garantizada por un teorema de convergencia global como podría estarlo en los métodos de falsa posición o de bisección. Así, es necesario partir de una aproximación inicial próxima a la raíz buscada para que el método converja y cumpla el teorema de convergencia local.
Estimación del Error
Se puede demostrar que el método de Newton-Raphson tiene convergencia cuadrática: si  es raíz, entonces:
es raíz, entonces:
 es raíz, entonces:
es raíz, entonces:
para una cierta constante  . Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
. Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
 . Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
. Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:
Error relativo entre dos aproximaciones sucesivas:
Con lo cual se toma el error relativo como si la última aproximación fuera el valor exacto. Se detiene el proceso iterativo cuando este error relativo es aproximadamente menor que una cantidad fijada previamente.
Teorema de Convergencia Local del Método de Newton
Sea ![f \in C^2 ([a,b])](http://upload.wikimedia.org/wikipedia/es/math/c/0/0/c00896b2abb4f364281706bf14896b25.png) . Si
. Si ![p \in [a,b]](http://upload.wikimedia.org/wikipedia/es/math/1/e/1/1e171f8b368d66602e04dbb52496b1cb.png) ,
,  y
y  , entonces existe un r>0 tal que si
, entonces existe un r>0 tal que si 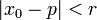 , entonces la sucesión xn con
, entonces la sucesión xn con  verifica que:
verifica que:
![f \in C^2 ([a,b])](http://upload.wikimedia.org/wikipedia/es/math/c/0/0/c00896b2abb4f364281706bf14896b25.png) . Si
. Si ![p \in [a,b]](http://upload.wikimedia.org/wikipedia/es/math/1/e/1/1e171f8b368d66602e04dbb52496b1cb.png) ,
,  y
y  , entonces existe un r>0 tal que si
, entonces existe un r>0 tal que si 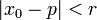 , entonces la sucesión xn con
, entonces la sucesión xn con  verifica que:
verifica que: para todo n y xn tiende a p cuando n tiende a infinito.
para todo n y xn tiende a p cuando n tiende a infinito.
Si además ![f \in C^3 ([a,b])](http://upload.wikimedia.org/wikipedia/es/math/0/2/e/02e1ee8032f272642b083bdb9ee1a9c0.png) , entonces la convergencia es cuadrática.
, entonces la convergencia es cuadrática.
![f \in C^3 ([a,b])](http://upload.wikimedia.org/wikipedia/es/math/0/2/e/02e1ee8032f272642b083bdb9ee1a9c0.png) , entonces la convergencia es cuadrática.
, entonces la convergencia es cuadrática.
Ejemplo
Consideremos el problema de encontrar un número positivo x tal que cos(x) = x3. Podríamos tratar de encontrar el cero de f(x) = cos(x) - x3.
Sabemos que f '(x) = -sin(x) - 3x2. Ya que cos(x) ≤ 1 para todo x y x3 > 1 para x>1, deducimos que nuestro cero está entre 0 y 1. Comenzaremos probando con el valor inicial x0 = 0,5
Los dígitos correctos están subrayados. En particular, x6 es correcto para el número de decimales pedidos. Podemos ver que el número de dígitos correctos después de la coma se incrementa desde 2 (para x3) a 5 y 10, ilustando la convergencia cuadrática.
En pseudocódigo, esto es:
function newtonIterationFunction(x) {return x - (cos(x) - x^3) / (-sin(x) - 3*x^2)}var x := 0,5for i from 0 to 99 {print "Iteraciones: " + iprint "Valor aproximado: " + xxold := xx := newtonIterationFunction(x)if x = xold {print "Solución encontrada!"break}}
Código en C
Programa escrito en C correspondiente al ejemplo f(x) = cos(x) - x3.
#include <stdio.h>#include <math.h>double FuncionIteracion(double x);int main() {int i;double x, xvieja;xvieja = 0.5; // valor inicialprintf("Iteracion valor\n");for(i=0; i<8; i++){x = FuncionIteracion(xvieja);xvieja = x;printf("%5.0d %20.12f\n", i+1, x);}return 0;}double FuncionIteracion(double x){double valorFuncion, funcionOriginal, funcionDerivada;funcionOriginal = cos(x) - pow(x, 3);funcionDerivada = -sin(x) - 3*pow(x, 2);valorFuncion = x - funcionOriginal / funcionDerivada;return valorFuncion;}
Para compilar en GNU/Linux con compilador de GNU, se escribe en una terminal:
$ gcc programa.c -lm -o programa
donde la opción -lm le indica al compilador que utilice la biblioteca de matemáticas.
Codigo en Matlab
Programa escrito en Matlab para hallar las raíces usando el método de NEWTON-RAPHSON
function x =newton()disp ('NEWTON-RAPHSON')xo=input('Valor inicial =');n=input ('numero de iteraciones=');salida=ones(n,4); % matiz de salida de datosfor i=1:nx1=xo-[(exp(-xo)-xo)]/[(-exp(-xo)-1)];vsal=[xo;x1];er=[[abs((xo-x1)/xo)]]*100; % error relativo porcentualea=[[abs((x1-xo)/x1)]]*100; % errorxo=x1;salida(i,1)=i;salida(i,2)=x1;salida(i,3)=er;salida(i,4)=ea;enddisp('ite raiz er ea');disp(num2str(salida));
El programa siguiente hace el cálculo para una superficie.
syms x1syms x2V=syms x3['sin(x1)+2^x2+log(x3)-7';'3*x1+2*x2-x3^3+1 ';'x1+x2+x3-5 '];%se calcula el jacobiano:DV(1,:)=[diff(V(1,:),x1), diff(V(1,:),x2),diff(V(1,:),x3)];DV(2,:)=[diff(V(2,:),x1), diff(V(2,:),x2),diff(V(2,:),x3)];DV(3,:)=[diff(V(3,:),x1), diff(V(3,:),x2),diff(V(3,:),x3)];%se da el valor de partida:x1=0;x2=4;x3=2;x_1o=[x1;x2;x3];%se calcula H en ese puntoVo(1,:)=eval(V(1,:));Vo(2,:)=eval(V(2,:));Vo(3,:)=eval(V(3,:));%Se calcula el Hessiano en ese puntoDV1=eval(DV);%se calcula la Inversa del Hessiano en ese puntoDV_1=DV1^-1;%se calcula el siguiente valor de iteraciónx_1=[x1;x2;x3]-DV_1*Vo;%cantidad de iteraciones maxima:n=50;%se define a = n, si se cumple condicion de error antes, cambiaa=n;for i=1:n%error relativo entre aproximaciones sucecivaser=norm(x_1-x_1o)/norm(x_1);if er<.0001a=i;'break;' endx1=x_1(1);x2=x_1(2);x3=x_1(3);x_1o=[x1;x2;x3];Vo(1,:)=eval(V(1,:));Vo(2,:)=eval(V(2,:));Vo(3,:)=eval(V(3,:));DV1=eval(DV);DV_1=DV1^-1;x_1=[x1;x2;x3]-DV_1*Vo;endax_1
Suscribirse a:
Entradas (Atom)